Remove Methods From Project

By atharvaparab9160

Problem Statement:

You are maintaining a project that has n methods numbered from 0 to n - 1.

You are given two integers n and k, and a 2D integer array invocations, where invocations[i] = [ai, bi] indicates that method ai invokes method bi.

There is a known bug in method k. Method k, along with any method invoked by it, either directly or indirectly, are considered suspicious and we aim to remove them.

A group of methods can only be removed if no method outside the group invokes any methods within it.

Return an array containing all the remaining methods after removing all the suspicious methods. You may return the answer in any order. If it is not possible to remove all the suspicious methods, none should be removed.

Example 1:

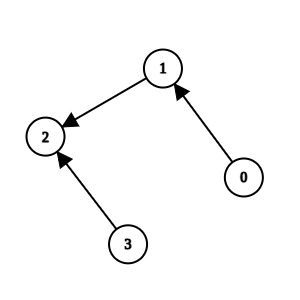
Input: n = 4, k = 1, invocations = [[1,2],[0,1],[3,2]]

Output: [0,1,2,3]

Explanation:

Method 2 and method 1 are suspicious, but they are directly invoked by methods 3 and 0, which are not suspicious. We return all elements without removing anything.

Example 2:

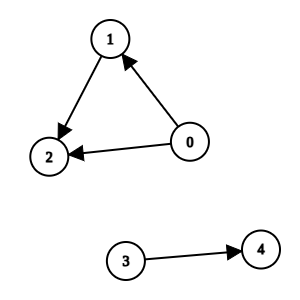
Input: n = 5, k = 0, invocations = [[1,2],[0,2],[0,1],[3,4]]

Output: [3,4]

Intuition :

Methods 0, 1, and 2 are suspicious and they are not directly invoked by any other method. We can remove them.

Complexity:

Time Complexity:

Building the Graph (Adjacency List) : O(m). DFS Traversal : O(n+m). Checking for External Dependencies : O(n+m). Total Time Complexity: The total time complexity is the sum of the three steps: O(m) + O(n + m) + O(n + m), which simplifies to O(n+m).

Space Complexity:

The space required is O(n + m) for the adjacency list and O(n) for the stack and suspicious array, so the total space complexity is O(n+m).

Solution:

def remainingMethods(n, k, invocations):
    # Initialize an adjacency list to represent the graph of method invocations
    adjacency_list = [[] for _ in range(n)]
    # Fill the adjacency list with the provided method invocations
    for invocation in invocations:
        adjacency_list[invocation[0]].append(invocation[1])
    # 'suspicious' will track whether a method has been invoked either directly or indirectly
    suspicious = [False] * n
    
    # Stack to perform DFS starting from the given k
    stack = deque([k])
    suspicious[k] = True
    # DFS to mark all reachable methods/node invoked either directly or indirectly starting from 'k'th method ( as k is given as suspicious )
    while stack:
        current_method = stack.pop()
        for connected_method in adjacency_list[current_method]:
            if suspicious[connected_method] == False:
                suspicious[connected_method] = True
                stack.append(connected_method)
    # Check if there are any nodes (methods/node) that could connect a suspicious node but are not suspicious themselves
    for method in range(n):
        if suspicious[method] == False:
            for connected_method in adjacency_list[method]:
                if suspicious[connected_method]:
                    # if we find any node which is connected to a suspicious then we return list of all nodes/mrthods
                    return list(range(n))
    # if we don't find any non suspicioius method connecting a suspicious method then Return the remaining non-suspicious methods/node
    remaining_methods = []
    for method in range(n):
        if suspicious[method] == False:
            remaining_methods.append(method)
    
    return remaining_methods

n = 4
k = 1
invocations = [[1,2],[0,1],[3,2]]

print(f" methods : {remainingMethods(n, k, invocations)}")
"""
INTUITION :

The problem can be seen as tracking how a buggy method (k) affects other methods in a project, which is like navigating a graph. Here's the simple intuition:

Graph Representation:
Each method is a node, and each invocation is a directed edge. If method a invokes method b, there's a directed edge from a to b.
Mark Suspicious Methods:
Start from the buggy method k and use DFS (depth-first search) to mark all methods that k directly or indirectly invokes as "suspicious."
Check for Dependencies:
Ensure no non-suspicious method depends on a suspicious one. If such a dependency exists, we can't safely remove anything.
Final Output:
If no external dependencies are found, return the remaining safe methods (those not marked suspicious).
In short: We find all methods affected by the buggy one using DFS, then check if it’s safe to remove them based on external dependencies.
"""